Conservation of Angular Momentum

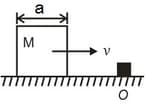
A cubical block of side $30 \mathrm{cm}$ is moving with velocity $2 \mathrm{m} {\mathrm{s}}^{-1}$ on a smooth horizontal surface. The surface has a bump at a point $O$ as shown in the figure. The angular velocity (in $\mathrm{rad} {\mathrm{s}}^{-1}$) of the block immediately after it hits the bump, is:

A child is standing with folded hands at the centre of a platform rotating about its central axis. The kinetic energy of the system is $K$. The child stretches his arms so that the moment of inertia of the system doubles. The kinetic energy of the system now is

A solid sphere is rotating in free space. If the radius of sphere is increased keeping mass same which one of the following will not be affected?

Relation between Torque and angular momentum is similar to the relation between

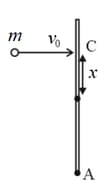
A uniform rod $\mathrm{AB}$ of length$L$ and mass $M$is lying on a smooth table. A small particle of mass $m$ strikes the rod with velocity $v_0$ at point $C$ at a distance $x$from the centre $O$. The particle comes to rest after collision. If the value of $x$, so that the point $\mathrm{A}$of the rod remains stationary just after the collision, is$L/n$, then find $n$.

Relation between Torque and angular momentum is similar to the relation between

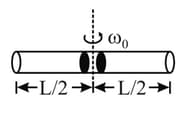
As shown in the figure, two balls of same mass $m$ are situated at the centre of a tube of mass $M$ and are rotating with a uniform angular velocity ${\omega }_0.$ If the balls suddenly come to end of the tube the resultant angular velocity will be :

Under the influence of the Coulomb field of charge $+Q,$ a charge $-q$ is moving around it in an elliptical orbit. Find out the correct statement.

A disc is free to rotate about a smooth horizontal axis passing through its centre of mass. A particle is fixed at the top of the disc. A slight push is given to the disc and it starts rotating. During the process

A time varying torque $\left(4t\right) \mathrm{N} \mathrm{m}$ is applied on an object about a pivot. Change in angular momentum of body till time $t=3\mathrm{ }\mathrm{s}$ is:

A thin circular ring of mass $M$ and radius $R$ is rotating about its axis with a constant angular velocity $\omega .$ Two objects each of mass $m,$ are attached gently to the opposite ends of a diameter of the ring. The ring now rotates with an angular velocity

A rigid metallic sphere is spinning around its own axis in the absence of external torque. If the temperature is raised, its volume increases by $9 \%$. The change in its angular speed is

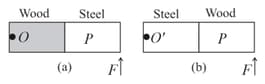
In the figure half of the meter scale is made of wood while the other half is of steel. In figure $\left(a\right)$ the wooden part is pivoted at $O$. A force $F$ is applied at the end of the steel part. In figure $\left(b\right)$ the steel part is pivoted at $O^{\text{'}}$ and the same force is applied at the wooden end.

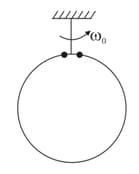
If net torque acting on a system is zero, then

A larger ring of mass $M$ and two small rings of mass $m$ start rotating with angular velocity ${\omega }_0^{}$ from the position as shown in figure. Initially small rings are close to axis. There is no friction at any contact surface. Then as time passes. (Consider the motion of small rings till they move up to the bottom most point)

A thin and circular disc of mass $M$ and radius $R$ is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity $\omega .$ If the another disc of same dimensions but of mass M/4 is placed gently on the first disc co-axially, then the new angular velocity of the system is:-

A uniform rod $AB$ of mass $m$ and length $l$ is at rest on a smooth horizontal surface. An impulse $P$ is applied to the end $B$. The time taken by the rod to turn through a right angle is

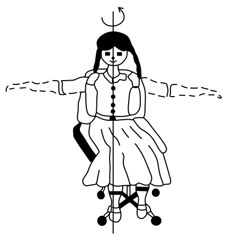
If frictional force is neglected and girl bends her hand, then (initially girl is rotating on chair)

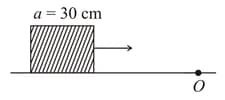
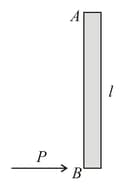
There is a cubical block with length of its side being $a$. It is moving with a velocity $v$ on a horizontal smooth plane as shown. It hits a ridge at point O. The angular speed of the block after it hits O is

If Bohr's quantization postulate (angular momentum $=\frac{nh}{2\pi }$) is a basic law of nature, it should be equally valid for the case of planetary motion also. Consider earth & sun system and apply Bohr's quantization postulate. If $n$ can be written as $\alpha \times {10}^{\beta }$, where $2<\alpha <3$ then find the value of $\beta$. The value of $\beta$ is the reason we never speak about quantization of orbits of planets around the sun.

Given: $m_{earth}=6\times {\mathrm{10}}^{\mathrm{24}}$, $v_{earth}=30,000 \mathrm{m} {\mathrm{s}}^{-1}$ and $r_{earth-sun}=1.49\times {10}^{11} \mathrm{m}$